Cover image credit: “Sequence…” by Diego3336 is licensed under CC BY 2.0.
When is interest earned and forfeited
We already know that keeping our expenses below our income is necessary for financial sustainability. Most of us default to keeping our savings as cash in our bank accounts, such as a checking account or current account. The savvy ones among us, in an effort to earn more interest on their savings, open a savings or money market account and park our savings in that account, since such accounts tend to offer a higher interest rates1. The even more savvier ones, in pursuit of higher interest rates, might take some of their cash that they don’t need immediately, and put it into what’s commonly known as CD (Certificate of Deposit) or Fixed Deposit (FD) accounts2, which advertise a higher interest rate than even savings accounts. Typically for all these types of accounts, interest is computed as “compound interest”, whereas for the latter accounts early withdrawal incurs a penalty, which is usually computed as the “simple interest” over the remaining term. How does compound interest differ from simple interest and, how exactly is the amount of interest computed?
Two types of interest
In finance, interest is computed over a specified time period, e.g., one year, and correspondingly, the interest rate is typically expressed as an APY.
There are two formulas used for computing interest, viz., the formula for simple interest and the formula for compound interest.
Simple interest definition
The formula for computing simple interest is indeed quite simple.
The simple interest on a given initial amount, a.k.a., “principal” over any single time period is directly proportional to the principal.
In other words, the simple interest earned in an account with an interest rate of $R$% per time period over a single time period on an principal amount of $P$ LCU is given by:
$$ \begin{equation} I = P \times R \end{equation} $$
It follows that the total simple interest accumulated in that account over $N$ time periods will be given by:
$$ \begin{equation} I = (P \times R) + (P \times R) + \ldots (N \textrm{times}) = P \times R \times N \end{equation} $$
This shows that the simple interest accumulated over a given time period is directly proportional to the time period.
Relation between simple interest & arithmetical progression
It is interesting to look at the evolution of the total amount over time in an account that accumulates simple interest3. In the beginning, we start with the principal, $P$ LCU. After one time period, the account will earn simple interest and the total amount in that account will be given by $(P+I)$ LCU, where $I$ is given by eq.(1). After the end of the second time period, the account will earn simple interest given by eq.(1) again, and the total amount in that account will be $P+I+I=(P+2\times I)$ LCU. Continuing like this, it’s easy to see that the evolution of the total amount in that account at the end of each successive time period is given by the sequence:
$$ \begin{equation} P, P + I, P + 2\times I, P + 3 \times I, \ldots \end{equation} $$
The sequence above is an example of what’s mathematically known as an “arithmetical progression”. As you can see, the defining feature of such a sequence is that successive term is the sum of the previous term and a constant number (in this case, $I$).
Compound interest definition
The formula for computing compound interest is also quite simple actually. In this case, the interest for a given time period is directly proportional to, not on the initial amount as in the case of simple interest, but rather to the total amount at the end of the previous time period. So, if we start off with an initial amount of $P$ LCU in an account with interest rate $R$% per time period, the interest at the end of the first time period will be:
$$ \begin{equation} I = P \times R \end{equation} $$
which is the same as in the case of simple interest4.
The total amount in LCU at the end of the first time period is, thus, $P+I = P+P\times R = P \times (1+R)$. The interest at the end of the second time period is computed on this amount, and therefore is given by:
$$ \begin{equation} I = P \times (1 + R) \times R \end{equation} $$
which, as you can see by comparison with eq. (2)5, is different from the case of simple interest.
Relation between compound interest & geometrical progression
It’s interesting to contrast how the total amount evolves in the case of compound interest to the case of simple interest. We already saw that the total amount accumulated by compound interest at the end of the first time period is $P \times (1+R)$ LCU. At the end of the second time period, the total amount (in LCU) is this amount plus the interest accumulated in the second time period, which is given by eq. (5), i.e.,
$$ \begin{equation} P \times (1+R) + P \times (1+R) \times R = P \times (1+R) \times (1+R) = P \times (1+R)^2 \end{equation} $$ Continuing like this, it’s easy to see that at the end of $N$ time periods, the total amount in the case of compound interest is $P \times (1+R)^N$ LCU. Thus, the sequence of evolution of the total amount in the case of compound interest is given by:
$$ \begin{equation} P, P \times (1+R), P \times (1+R)^2, \ldots \end{equation} $$
The sequence above is an example of what’s mathematically known as a “geometric progression”. As you can see, the defining feature of this sequence is that each term of the sequence is obtained by multiplying the previous term by a constant number (in this case, $(1+R)$ is the constant multiple).
Comparison of growth rates of simple and compound interest
From eq.(2), we see that the total simple interest accumulated over $N$ time periods is given by $P \times R \times N$ LCU. Therefore, the total amount after $N$ time periods will be $P + P \times R \times N = P \times (1 + R \times N)$ LCU. In comparison, we saw earlier that the total amount in the case of compound interest after $N$ time periods is given by $P \times (1+R)^N$ LCU.
Thus, we see that the total amount grows linearly with the number of time periods in the case of simple interest, but exponentially with the same quantity in the case of compound interest.
The graph below shows the evolution of the total amount in the case of simple interest vs. compound interest for an example initial amount of $P=1000$ LCU, and $R=10$% over $N=11$ time periods.
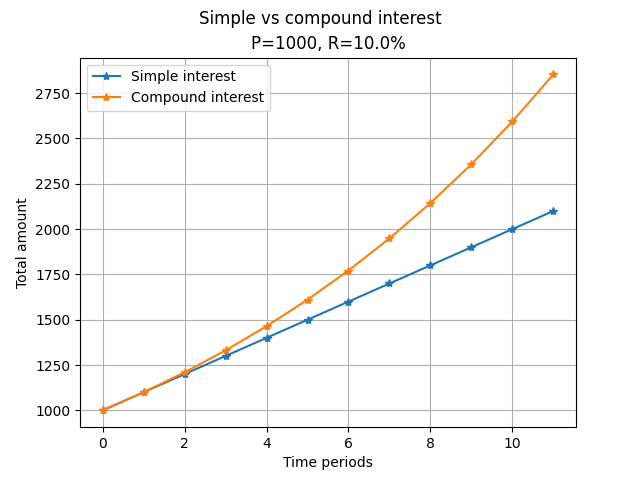
It is clear from the graph above that the total amount grows much more rapidly in the case of compound interest than in the case of simple interest. This graph shows succinctly how compound interest can allow you to accumulate more and more money with each successive time period, thereby acting as a powerful propeller towards achieving riches.
